Symmetrie und Magie

Wer kennt es nicht: Für irgendein Ritual muss ein Kreis, Quadrat oder ein Pentagramm auf dem Ritualplatz gezeichnet werden. Doch das, was man dann später auf dem Boden bewundern kann, ähnelt eher einem Malgebilde aus dem Kindergarten, zumindest der Symmetrie nach.

Hierfür gibt es aber eine ganz einfache Lösung, damit man seine Pentagramme auch sauber zeichnen kann: Einfach irgendeine Holzplatte - alternativ dazu tut es auch dickes Leder - nehmen, in die Mitte einen Nagel (eine Niete) hämmern und daran etwas Schnur befestigen.

Jetzt braucht man nur noch daheim mit Zirkel und Lineal die entsprechenden Winkel für ein Pentagramm, Heptagramm, was man auch immer will, auf der Holzplatte vorzeichnen, und kann dann mit Hilfe der Schnur das Ganze in beliebiger Länge auf den Boden bringen.--TobiasSeybold

Alternativ könnte man zu einem Radius passende Längen für die Bogensehnen (die dann das Polygon bilden) auf der Schnur durch Knoten abtragen. Dann spart man sich die Scheibe, kann aber nur eine Größe.--RalfHüls, 10.12.2003

90°-Winkel bekommt man hin, indem man in eine Schnur in gleichen Abständen Knoten macht. Da 3^{2 + 4}2 = 5^2, haben wir dank Pythagoras ganz leicht einen rechten Winkel. Alternativ nimmt man sich auf einer Geraden (entlang einer gespannten Schnur gezeichnet) zwei beliebige Punkte, schlägt um diese Kreise (deren Radien größer sind als der Abstand der Punkte zueinander) und hat durch die Schnittpunkte der Kreise eine Gerade im rechten Winkel auf die erste Gerade. --Garou, 10.12.2003

Sechsecke bekommt man indem man einen Kreis zeichnet, durch den Mittelpunkt des Kreises eine gerade zieht und vom Schnittpunkt der Geraden mit dem Kreis nochmal den Radius des ursprünglichen Kreises anträgt. Sieht dann ungefähr so aus: 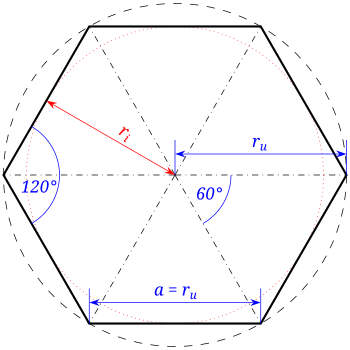Für den dens intressiert: Die Geometrie dahinter ist einfach das sich das Sechseck in sechs Gleichseitige Dreiecke zerlegen läßt. --TobiKremer 13.09.2007

zurück zu LarpMagie